numba 0.11.0 documentation
Open Table Of Contents

Table Of Contents

Previous topic

Numba Roadmap

Next topic

Numba Module Reference

This Page

Table Of Contents

Previous topic

Numba Roadmap

Next topic

Numba Module Reference

This Page

Development crash course

This document describes a short crash-course for numba development, where things are and where we want them at.

Overview

We start with a Python AST, compiled from source code or decompiled from bytecode using meta. We run a series of stages that transform the program as an AST to something from which we can generate code. The pipeline and environment are central pieces in this story:

Stages

The main stages are:

  • Control flow analysis: numba/control_flow

    This builds a Control Flow Graph from the AST and computes the SSA graph for the variable definitions. In this representation, each variable assignment is a definition, e.g.:

    x = 0         # definition 1
x = "hello"   # definition 2

    Assignments and variable references are recorded as abstract statements in the basic blocks of the CFG, such as

    • numba.control_flow.cfstats.NameAssignment
    • numba.control_flow.cfstats.NameReference
    • numba.control_flow.cfstats.PhiNode

    The phi node occurs at control flow joint points, e.g. after an if-statement, or in the condition block of a loop with a loop-carried dependency for a variable:

    if c:
    x = 0
else:
    x = 2
# phi here

    and:

    x = 0
for i in range(N):  # phi in condition block: x_1 = phi(x_0, x_2)
    x = x + i # loop-carried dependency

    The phi nodes are themselves variable definitions, and they define the points where variables merge and need a unifyable type (e.g. (int, int), or (int, float), as opposed to (int, string)).

  • Type inference: numba.type_inference

    Infer types of all expressions, and fix the types of all local variables. This operates in two stages:

    • Infer types for all local variable definitions (including phis)

      For an overview of this see Type Dependence Graph Construction below.

    • Now that all variable definitions have a type, we can easily infer types for all expressions by propagating type information up the tree

    When the type inferencer cannot determine a type, such as when it
    calls a Python function or method that is not a Numba function, it
    assumes type object. Object variables may be coerced to and from
    most native types.
    The type inferencer and other code insert CoercionNode nodes that
    perform such coercions, as well as coercions between promotable
    native types.
    It also resolves the return type of many math functions called
    in the numpy, math and cmath modules.
    Each AST expression node has a Variable that holds the type of
    the expression, as well as any meta-data such as constant values
    that have been determined.
    To see how builtins, math and numpy callables are handled, have
    a read through Adding Type Inference for External Code in the user documentation,
    as well as numba.type_inference.modules::
    This above sub-package is an important part of numba that
    infers (and sometimes grossly rewrites) calls to known functions.

  • Specialization/Lowering: numba/specialize and numba/transforms.py

    What follows over the typed code are a series of transformations to lower the level of the code into something low-level - something amenable to code generation:

    • Rewrite loops over range or xrange into a while loop with a counter

    • Rewrite iteration over arrays to a loop over range with an index into the array

    • Lower object conversions into calls into the Python C-API. For instance it resolves coercions to and from object into calls such as PyFloat_FromDouble, with a fallback to Py_BuildValue/PyArg_ParseTuple.

    • Lower exception code into calls into the C-API and insert NULL pointer checks in places

    • Normalize comparisons (e.g. a < b < c => a < b and b < c)

    • Keep track of refcounts. This is mostly done with ObjectTempNode, which hold a temporary for an object (a new reference). These temporaries are decreffed at cleanup:

      define double @func()  {
entry:
  %retval = alloca double           ; return value
  %tmp = alloca object              ; object temporary
  ...
  %obj = call PyObject_SomeNewObject()
  %have_error = cmp obj NULL        ; check return value
  cbranch %have_error, label %error, label %success

success:                            ; no error
  do something interesting with %obj
  store %something %retval          ; return some value
  br return_block                   ; ok, we're done

error:                              ; some error occurred :(
  store NaN retval
  br cleanup

return_block:                       ; clean up objects
  call void Py_XDECREF(%0)
  %result = load %retval
  ret %result                       ; return result
}

  • Code generation: numba/codegen

    Generate LLVM code from the transformed AST. This is relatively straightforward at this point. One tricky problem is that the basic blocks from the LLVM code no longer correspond to the basic blocks of the CFG, since error checks have been inserted. This makes tracking phis harder than it should be.

    The code generator uses utility functions from numba/utility and numba/external to do things like refcounting (Py_INCREF, etc) and uses helpers to slice and broadcast arrays.

Package Structure

  • numba/type_inference

    Type inference

  • numba/typesystem

    Numba typesystem, see also Types and Variables

  • numba/specialize

    Lowering transformations, along with numba/transforms.py . Coercions are in numba/transforms.py

  • numba/nodes

    Contains AST nodes. Some nodes that need some explaining:

    • ObjectTempNode:

      Holds a PyObject * temporary that it manages a refcount for

    • CloneNode/CloneableNode:

      These nodes are used for subtree sharing, to avoid re-evaluation of the subtree. Consider e.g. the expression ‘x * 2’, which we want to refer to twice, but evaluate once. We can do the following:

      cloneable = CloneableNode(<x * 2 expression>)
clone  = CloneNode(cloneable)

      Here cloneable must be evaluated before clone. We can now generate as many clones as we want without re-evaluating x * 2

  • numba/exttypes

    Numba extension types, have a read through Extension Types (Classes) first. These are fairly well documented. To see how they work, see below Extension Classes

  • numba/closures

    Implements closures for numba. See Closures and closureimpl below for how they work.

  • numba/support

    Ctypes, CFFI and NumPy support (slicing, etc)

  • numba/array_expressions.py

    Implements array expressions using minivect. Since we don’t actually use the tiling specializers or desperately need crazy optimizations for special cases, we should really use lair’s loop_nest instead and throw away numba/minivect

  • numba/vectorize

    The @vectorize functionality to build (generalized) ufuncs

  • numba/wrapping

    Entry points to compile numba functions, classes and methods

  • numba/utility and numba/external

    Runtime support utilities. And yes, you make a valid point, this should really be one package.

  • numba/intrinsic

    Intrinsics and instruction support for numba, as well as... internal intrinsics. Merge internal stuff in numba/external :)

    See Using Intrinsics for what intrinsics do.

  • numba/containers

    Numba typed containers, see Typed Containers

  • numba/asdl and numba/ir

    Utilities to validate ASTs and generate fast visitors/AST implementations from ASDL. This should be factored out into asdlpy or somesuch.

  • numba/viz

    Format ASTs and CFGs with graphviz. See also the ‘annotate’ branch

  • numba/minivect

    Array expression compiler. numba.array_expressions is the only remaining module depending on this. However, since none of the optimizations are actually used, it doens’t make sense to keep this. Instead we can use the loop_nest function from the lair project.

    More on how the array expressions work: Array Expressions

Type Dependence Graph Construction

From the SSA graph we compute a type graph by inferring all variable assignments. This graph often has cycles, due to the back-edge in the CFG for loops. For instance we may have the following code:

x = 0
for i in range(10):
    x = f(x)

y = x

Where f is an external autojit function (i.e., it’s output type depends on it’s dynamic input type).

We get the following type graph:

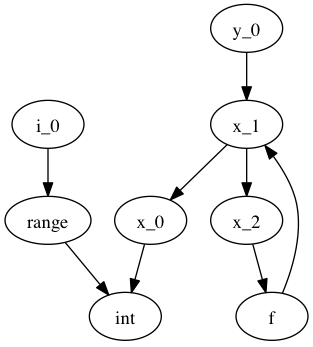
digraph typegraph { x_0 -> int x_1 -> x_0 x_1 -> x_2 x_2 -> f f -> x_1 y_0 -> x_1 i_0 -> range range -> int }

Below we show the correspondence of the SSA variable definitions to their basic blocks:

digraph cfg { "entry: [ x_0, i_0 ]" -> "condition: [ x_1 ]" -> "body: [ x_2 ]" "body: [ x_2 ]" -> "condition: [ x_1 ]" "condition: [ x_1 ]" -> "exit: [ y_2 ]" }

Our goal is to resolve this type graph in topological order, such that we know the type for each variable definition (x_0, x_1, etc).

In order to do a topological sort, we compute the condensation graph by finding the strongly connected components and condensing them into single graph nodes. The resulting graph looks like this:

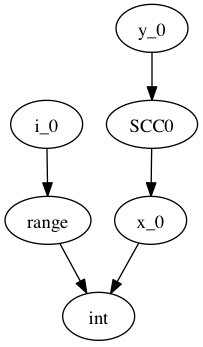
digraph typegraph { x_0 -> int SCC0 -> x_0 y_0 -> SCC0 i_0 -> range range -> int }

And SCC0 contains the cycle in the type graph. We now have a well-defined preorder for which we can process each node in topological order on the transpose graph, doing the following:

  • If the node represents a concrete type, propagate result along edge
  • If the node represents a function over an argument of the given input types, infer the result type of this function
  • For each SCC, process all internal nodes using fixpoint iteration given all input types to the SCC. Update internal nodes with their result types.

Closures

numba/closures.py provides support for closures and inner functions:

@autojit
def outer():
    a = 10 # this is a cellvar

    @jit('void()')
    def inner():
        print a # this is a freevar

    inner()
    a = 12
    return inner

The ‘inner’ function closes over the outer scope. Each function with cellvars packs them into a heap-allocated structure, the closure scope.

The closure scope is passed into ‘inner’ when called from within outer.

The execution of def creates a NumbaFunction, which has itself as the m_self attribute. So when ‘inner’ is invoked from Python, the numba wrapper function gets called with NumbaFunction object and the args tuple. The closure scope is then set in NumbaFunction.func_closure.

The closure scope is an extension type with the cellvars as attributes. Closure scopes are chained together, since multiple inner scopes may need to share a single outer scope. E.g.:

def outer(a):
    def inner(b):
        def inner_inner():
            print a, b
        return inner_inner

    return inner(1), inner(2)

We have three live closure scopes here:

scope_outer = { 'a': a }  # call to 'outer'
scope_inner_1 = { 'scope_outer': scope_outer, 'b': 1 } # call to 'inner' with b=1
scope_inner_2 = { 'scope_outer': scope_outer, 'b': 2 } # call to 'inner' with b=2

Function ‘inner_inner’ defines no new scope, since it contains no cellvars. But it does contain a freevar from scope_outer and scope_inner, so it gets scope_inner passed as first argument. scope_inner has a reference to scope outer, so all variables can be resolved.

These scopes are instances of dynamic numba extension classes.

Extension Classes

Extension classes live in numba/exttypes.

@jit

Compiling @jit extension classes works as follows:

  • Create an extension Numba type holding a symbol table

  • Capture attribute types in the symtab ...

    • ... from the class attributes:

      @jit
class Foo(object):
    attr = double

    • ... from __init__:

      @jit
class Foo(object):
    def __init__(self, attr):
        self.attr = double(attr)

  • Type infer all methods

  • Compile all extension methods

    • Process signatures such as @void(double)
    • Infer native attributes through type inference on __init__
    • Path the extension type with a native attributes struct
    • Infer types for all other methods
    • Update the ext_type with a vtab type
    • Compile all methods

  • Create descriptors that wrap the native attributes

  • Create an extension type:

    {

    PyObject_HEAD ... virtual function table (func **) native attributes

    }

The virtual function table (vtab) is a ctypes structure set as attribute of the extension types. Objects have a direct pointer for efficiency.

@autojit

Compiling @autojit extension classes works as follows:

  • Create an extension Numba type holding a symtab

  • Capture attribute types in the symtab in the same was as @jit

  • Build attribute hash-based vtable, hashing on (attr_name, attr_type).

    (attr_name, attr_type) is the only allowed key for that attribute (i.e. this is fixed at compile time (for now). This means consumers will always know the attribute type (and don’t need to specialize on different attribute types).

    However, using a hash-based attribute table allows easy implementation of multiple inheritance (virtual inheritance), without complicated C++ dynamic offsets to base objects (see also virtual.py).

For all methods M with static input types:
  • Compile M
  • Register M in a list of compiled methods

  • Build initial hash-based virtual method table from compiled methods

  • Create descriptors that wrap the native attributes

  • Create an extension type:

    {
    hash-based virtual method table (PyCustomSlots_Table **)
    PyGC_HEAD
    PyObject_HEAD
    ...
    native attributes
}

    We precede the object with the table to make this work in a more generic scheme, e.g. where a caller is dealing with an unknown object, and we quickly want to see whether it support such a perfect-hashing virtual method table:

    NOTE: What we want is to actually use a separate attribute table

    in addition to the virtual method table, giving all extension objects a compatible layout.

    if (o->ob_type->tp_flags & NATIVELY_CALLABLE_TABLE) {
    PyCustomSlots_Table ***slot_p = ((char *) o) - sizeof(PyGC_HEAD)
    PyCustomSlots_Table *vtab = **slot_p
    look up function
} else {
    PyObject_Call(...)
}

    We need to store a PyCustomSlots_Table ** in the object to allow the producer of the table to replace the table with a new table for all live objects (e.g. by adding a specialization for an autojit method).

Wrappers

There are several wrappers in numba that wrap functions, classes and methods. The key implementations are in:

  • numba/numbawrapper.pyx
  • numba/numbafunction.c
  • numba/codegen/llvmwrapper.py

What numba does is it creates a function like this (in C pseudo-code):

double square(double arg) {
    return arg * arg;
}

and it wraps it as follows:

PyObject *square_wrapper(PyObject *self, PyObject *args) {
    double arg;

    if (!PyArg_ParseTuple(args, "d", &arg))
        return NULL;

    return PyFloat_FromDouble(square(arg));
}

The wrapper is a CPython compatible function the likes of which you often see in extension modules. It is created by llvmwrapper.py. This wrapper is turned into an PyCFunctionObject, defined in Include/methodobject.h in CPython’s source tree:

typedef struct {
    PyObject_HEAD
    PyMethodDef *m_ml; /* Description of the C function to call */
    PyObject    *m_self; /* Passed as 'self' arg to the C func, can be NULL */
    PyObject    *m_module; /* The __module__ attribute, can be anything */
} PyCFunctionObject;

Numba uses a wrapper (a subclass) of PyCFunctionObject, called numbafunction, which has some extra fields and gives the function a more pythonic interface, such as a dict, a way to override __doc__, etc. It also has a field to hold a closure frame (see Closures).

This function object is created after compilation of the function and its wrapper (square_wrapper). It is instantiated in llvmwrapper.py:numbafunction_new, calling NumbaFunction_NewEx.

@jit

Jit functions are wrapped typically by the NumbaFunction in numbafunction.c. The NumbaCompiledWrapper is only a temporary wrapper used in case of a recursive function that is still being compiled, and for which we have no pointer.

@autojit

Autojit functions are handled by NumbaSpecializingWrapper, which wraps a Python function and when called does a lookup in a cache to see if a previously compiled version is available. This code in in numbawrapper.pyx.

NumbaSpecializingWrapper holds an AutojitCache which tries to find a match very quickly. However, it may not always find a compiled version even though it’s in the cache, for instance because there are values of different Python types which are represented using the same numba type.

This is then corrected by a slower path which tries to compile the function, and creates a type for each argument. It uses these types to do a lookup in numba.functions.FunctionCache.

classes

The story for classes is slightly different. @jit classes are simply turned into a compiled extension type, with compiled methods set as class attributes. The NumbaFunction handles binding to bound or unbound methods.

@autojit classes are wrapped in the same way as autojit functions, but with a different compiler entry point that triggers when the wrapper is called. The entry point compiles a special version of the extension class, and any methods that are not specialized (e.g. because they take further arguments than self), are wrapped by wrappers (again NumbaSpecializingWrapper) that compile a method on call and update the method table (the table supporting fast call from numba space).

The only special case are unbound methods, consider the code below:

from numba import *

@autojit
class A(object):
    def __init__(self, arg):
        self.arg = arg

    def add(self, other):
        return self.arg * other

print A(10).exttype     # <AutojitExtension A({'arg': int})>
print A(10.0).exttype   # <AutojitExtension A({'arg': float64})>

We have two versions of our extension type, one with arg = int and one with arg = float64. Now consider calling add as an unbound method:

print A.add(A(10.0), 5.0)   # 50.0

To dispatch from unbound method A.add of unspecialized class A to specialized method A[{'arg':int_}].add, numba creates a UnboundDelegatingMethod defined in numba.exttypes.autojitclass.

Array Expressions

Array expressions live in numba.array_expressions. Array expressions roughly work as follows:

  • Detect array expressions (ArrayExpressionRewrite)

    This code finds a maximal sub-expression that operates on arrays, e.g. A + B * C. These expressions are captured via register_array_expression.

  • The registered expression is extracted using get_py_ufunc_ast. This function traverses the subexpression and does the following:

    • demote types from arrays to scalars
    • register any non-array sub-expression of our expression as an operand. More on this below.

  • Compile the extracted sub-expression as a seprate function

  • Generate a loop nest using minivect that calls this compiled function

Let’s walk through an example, consider for argument’s sake the following expression:

A + sin(B) * g(x)

Where g(x) returns a scalar and is not part of the array expression. Our AST looks like this:

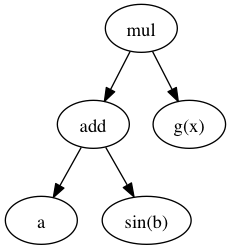
digraph expr { mul -> add mul -> "g(x)" add -> a add -> "sin(b)" }

We take this expression and build a function with g(x) as operand:

def kernel(op0, op1, op2):
    return op0 + sin(op1) * op2

Each operation acts on scalars. Note that the g(x) is not part of the kernel. We now use minivect to generate a loop nest, e.g. for 2D arrays:

def loop_nest(shape, result, A, B, g_of_x):
    for i in range(shape[0]):
        for j in range(shape[1]):
            result[i, j] = kernel(A[i, j], B[i, j], g_of_x)

Result is allocated, or in cases of slice assignment it is the LHS:

LHS[:, :] = A + sin(B) * g(x)

The passed in shape is the broadcasted result of the shapes of A and B:

shape = broadcast(A.shape, B.shape)
result = np.empty(shape)
loop_nest(shape, result, A, B, g(x))

Testing

Whenever you make changes to the code, you should see what impact this has on by running the test suite:

$ python runtests.py                # run whole test suite
$ python runtests.py mypackage      # run tests under mypackage
$ python runtests.py mypkg.mymod    # run test(s) matched by mypkg.mymod

The test runner matches by substring, i.e.:

$ python runtests.py conv
Running tests in /home/mark/numba/numba/numba
numba.tests.test_object_conversion                                     SUCCESS
numba.typesystem.tests.test_conversion                                 SUCCESS

To isolate problems it’s best to create an isolated test-case that is as small as possible yet still exhibits the problem, often using just a simple test script.

Debugging compiler tracebacks can be handled through prints, but if the problem is less obvious (or the codebase unfamiliar) it is often simpler to use post-mortem debugging, which can help understand what’s going wrong without modifying any code (and later tracking down print statements that you accidentally committed):

$ python -m pdb test.py

When using post-mortem debugging it’s useful to enable the post-mortem option in numba.environment.FunctionErrorEnvironment:

enable_post_mortem = TypedProperty(
    bool,
    "Enable post-mortem debugging for the Numba compiler",
    False
)

Set the default value to True there. This way exceptions are not swallowed and accumulated (and hence raised from the error reporter, instead of the failing place in the compiler).

Debugging

Depending on the nature of the problem, there are some tools available for debugging what’s going on. In the annotate branch there is functionality to debug pretty-print to the terminal, create a graphviz visualization or generate a webpage:

usage: numba [-h] [--annotate] [--dump-llvm] [--dump-optimized] [--dump-cfg]
         [--dump-ast] [--fancy]
         filename

positional arguments:
  filename          Python source filename

optional arguments:
  -h, --help        show this help message and exit
  --annotate        Annotate source
  --dump-llvm       Print generated llvm assembly
  --dump-optimized  Dump the optimized llvm assembly
  --dump-cfg        Dump the control flow graph
  --dump-ast        Dump the AST
  --fancy           Try to output fancy files (.dot or .html)

The --annotate feature also prints the types of each variable used in a certain expression.

Debugging ASTs

You get more control over when the AST is dumped by adding the dump_ast stage in numba.environment at the right place in the pipeline. If you just quickly want to debug print an AST from Python, there is:

  • ast.dump(mynode)
  • utils.pformat_ast or utils.dump

It can also help sometimes to look at an instance of the data of certain piece of code is dealing with interactively, to try and make sense of what is happening. You can do this with a breakpoint using your favorite Python debugger, e.g. import pdb; pdb.set_trace().

Debugging Types

Debugging types can be tricky, but something that is often valuable is numba.typeof:

@jit(...)
def myfunc(...):
    ...
    print(numba.typeof(x))
    print(numba.typeof(x + y))

You can also always force types through casts or locals:

@jit(..., locals={'x':double}) # locals
def myfunc(...):
    print(double(y))           # cast

Debugging the Translator

To debug the translator, one can again stick with prints or post-mortem debugging. If the latter option is desirable, make absolutely sure that you enable the post-mortem debug option (see post-mortem). This makes sure numba does not delete the LLVM function, which means the LLVM values referenced in the translator will still be in a consistent state.

Problems

There are several problems with the codebase, stemming from our IR. The AST is too high level for most of the operations that we need to do, and has too much information, which leads to code having to deal with different in-memory formats that are doing similar things - which should be encoded in a uniform way. Consider e.g. the following code:

x = range(N)
for i in x:
    ...

# And
for i in range(N):
    ...

The code that detects and transforms iteration over range should be written in a uniform way, depending on the flow of values irregardless of the syntax. Besides the level of information ASTs are not always amenable to transformations, e.g. when you want to execute some statements in the middle of an expression, or when you want to share a subtree (see the Clone(able)Node discussion above nodes).

Another issue is that refcounting and the Python C-API as well as NumPy are baked into the transformations. Coupling these APIs like this can be a real problem when you want to switch to a different runtime environment or library (CPython, NumPy).